A webglbasic egyik erőssége a geometria számítása matematikai képletekkel. A példában egy üvegből készült terráriumot fogok modellezni úgy, hogy minden adatot változókban, paraméterekben tárolok.
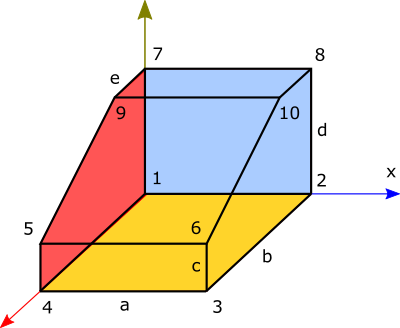
Célszerű először papíron vagy egy 2D rajzoló programmal lerajzolni a modellt. Ezután ráírtam a paraméterket. Ebben az esetben 5 db ilyen méret lesz lényeges:
a: szélesség
b: hosszúság
c: előlap magassága
d: magasság
e: tetőlap hosszúsága
Minden csúcs kap tetszőleges sorrendben egy sorszámot 1-től kezdődően. Ezek lesznek a felületek vertex pontjai.
Következő lépés a sík lapok háromszögekre bontása. Téglalapokat 2 db háromszögre lehet bontani, de az oldallapokat már 3 darabból kell összerakni.
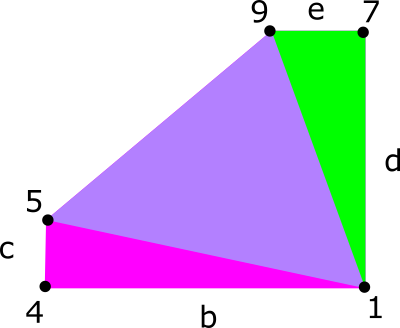
A felületeket a vertex pontok felsorolásával lehet megadni. Célszerű azonos irányban haladva (pl. jobbra) haladva felsorolni a pontokat!
|
Például az alsó négyszög háromszögei: |
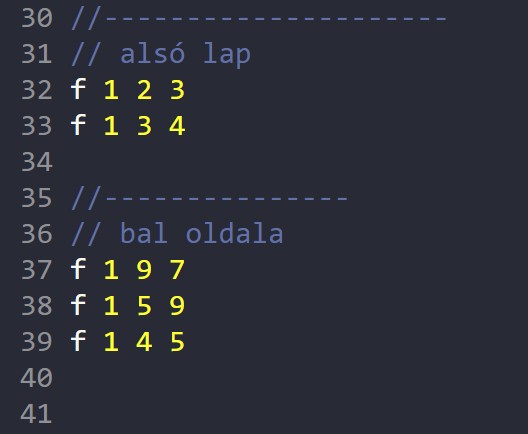
A baloldali lap háromszögei: 1 9 7, 1 5 9, és 1 4 5 |
A webglbasic kód elején megadjuk a paramétereket:

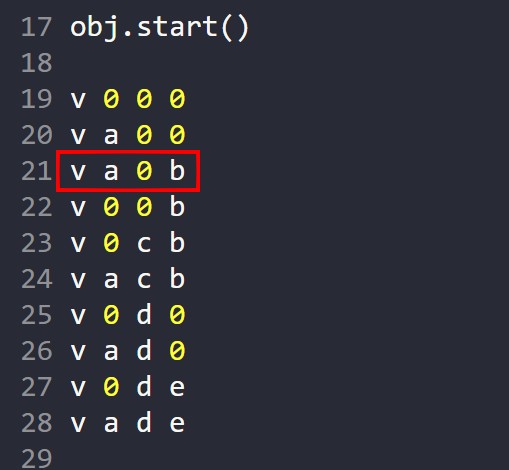
Ezután egy OBJ utasításban felsoroljuk a vertex pontokat. Az első pont sorszáma lesz 1. A pirossal jelölt sor a 3. pont koordinátái. A pont x,y,z koordinátái helyén számokat, és változókat is megadhatunk. Az adatokat csak 1 db szóköz válassza el egymástól!
 |
Ezután jöhetnek a felületek háromszögei:
|
A megfelelő nézőpont beállítása után beszúrhatunk a forrásba néhány kamera utasítást.

Végül lehet különböző paraméterekkel generálni a 3D modellt.
 |
 |
 |
A teljes kód:
color(#00bfff,#00bfff,#0,1,0.8)
a = 20
b = 10
c = 2
d = 10
e = 6
obj.start(2)
v 0 0 0
v a 0 0
v a 0 b
v 0 0 b
v 0 c b
v a c b
v 0 d 0
v a d 0
v 0 d e
v a d e
//---------------------
// alsó lap
f 1 2 3
f 1 3 4
//---------------
// bal oldala
f 1 9 7
f 1 5 9
f 1 4 5
//---------------
// jobb oldala
f 2 10 8
f 2 6 10
f 2 3 6
//---------------
// eleje
f 3 4 5
f 3 5 6
//---------------
// teteje
f 7 8 9
f 8 10 9
//---------------
// hátlap
f 1 7 2
f 7 8 2
obj.end
camera(KAM1, 25.66, 23.25, 41.04, 3.13, -0.74, -1.25)
camera(KAM2, -6.39, 30.53, 41.56, 8.37, -0.32, 0.31)