Támogatás
Az oldal oktatási célra készült, és folyamatosan fejlesztem, amikor időm engedi. A tárhelyet önerőből tartom fent, ezért bármilyen támogatással segítheted a további működést.
Paypal címem:
niethammer.zoli@gmail.com
AR marker
A marker egy olyan kép, amelyet a kiterjesztett valóság modellkhez használunk. Nyomtasd ki kb. 10-15 cm méretben, vagy nagyítsd ki egy monitoron!
A fordító rendelkezik egy fizikai szimulációs modullal, amely korlátozott mértékben képes a valós sebességeket, mozgásokat szimulálni egy tetszőleges gravitációs térben. Jelenleg a gömb, a téglatest, és a henger geometriák használhatók a szimulációhoz.
Első lépésként be kell állítani a gravitációs vektort, vagyis merre zuhanjanak a testek.
A példában lefelé irányuló 2 egység erősségű a gravitáció.
A fizika.start utasítás kapcsolja be a szimulációt. Amint lefordítod a kódot, a testek azonnal lefelé zuhannak, és meg sem állnak a végtelenig.
gravitáció(0, -2, 0)
fizika.start
hely(0,10,0)
tégla(2)
hely(-5,10,0)
gömb(1)
hely(5,10,0)
henger(1,1,2)
A NASA Shuttle Radar Topography programja során majdnem az egész Föld domborzatát felmérték radaros távolság méréssel. A teljes adatbázis ingyenesen elérhető 30 m pontossággal. Regisztráció után a nyers mérési adatok letölthetők, de a szövegfájlt fel kell dolgozni valamilyen szoftverrel. Van egy egyszerűbb út is, mivel az egyes térképészeti blokkok JPG formátumban is hozzáférhetők. Ezek szürke árnyalatos képek 3601x3601 pixeles méretben. Minél fehérebb egy pixel, annál magasabb az adott terület.
Interaktív online térképen böngészhetők a blokkok, és pár kattintással letölthetők a JPG állományok:
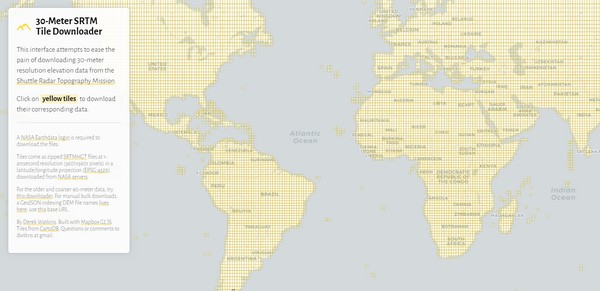
Az egérrel kinagyítva egy blokkot, már láthatók a fontosabb nevek, így könnyebb beazonosítani a helyet. A blokkra kattintva megnyitható a szürke árnyalatos JPG.
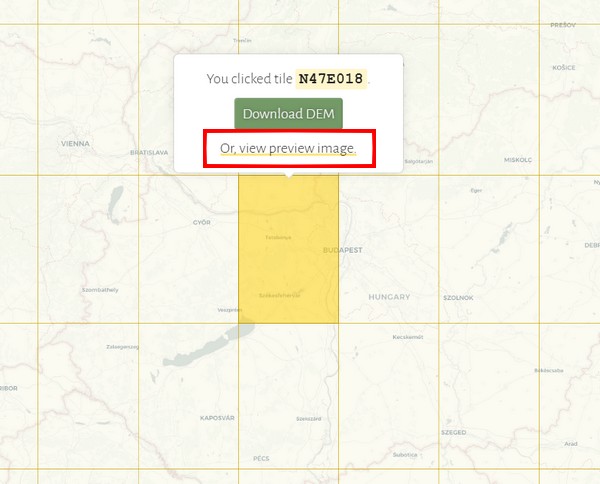
A képet másold át egy szerkesztőbe, majd vágd ki a lényeges részt. Itt most a Dunakanyar egy részlete volt a fontos.
Végül méretezd át úgy, hogy 400x400 pixelnél kisebb legyen a kép, majd tetszőleges néven, de PNG formátumban mentsd el!
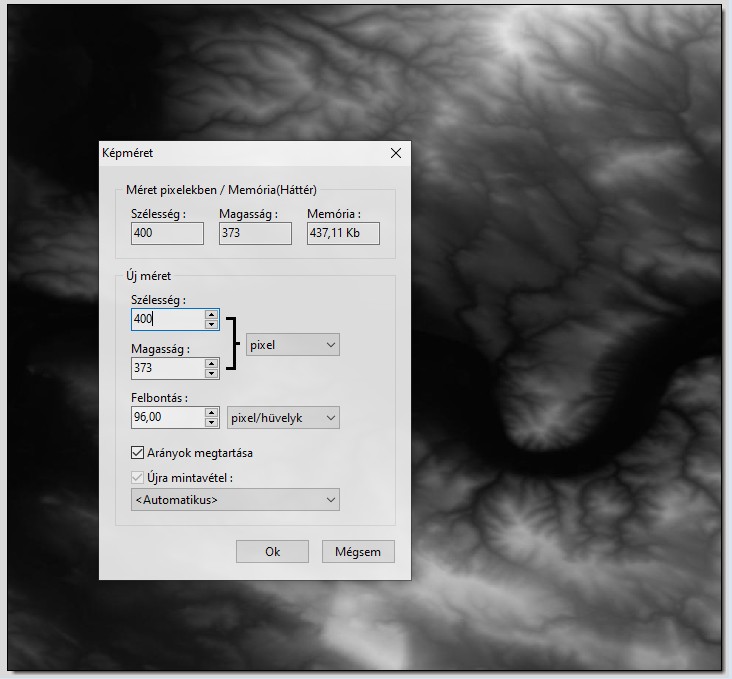
Ezt a PNG képek kell a saját tárhelyedre, vagy a TESZT tárhelyre feltölteni!
A PNG-re kattintva a következő utasítás kerül a baloldali editorba:
transparent.texture(/terraimage/dunakanyar.png, 1, 1,fiók_neve)
Írd át erre:
terra.image(/terraimage/dunakanyar.png, 20, 20,fiók_neve)
A fiók_neve helyen természetesen a te fiókód neve lesz automatikusan beírva.
A 20 egység a kész 3D térkép x, és y mérete lesz. A z irányú méretet a PNG szürke árnyalatából számítja a program. Szükség esetén korrigálható a MÉRET utasítással. Érdemes még az egész geometriát 90 fokkal elforgatni.
A teljes kód:
anyag(matt)
szín(szürke)
forgás(-90,0,0)
méret(1, 1, 0.6)
terra.image(/terraimage/dunakanyar.png, 20, 20,webglbasic)
camera(KAM1, 7.64, 18.96, 22.6, 0, 0, 0)
Kattints a képre!
Ha sikerül a NASA mappal közel azonos műholdképet találnod, akkor azt textúrának be is rakhatod a szürke szín helyett. A beépített textúrák között megtalálod a FUJI hegy mapját, és textúráját is.
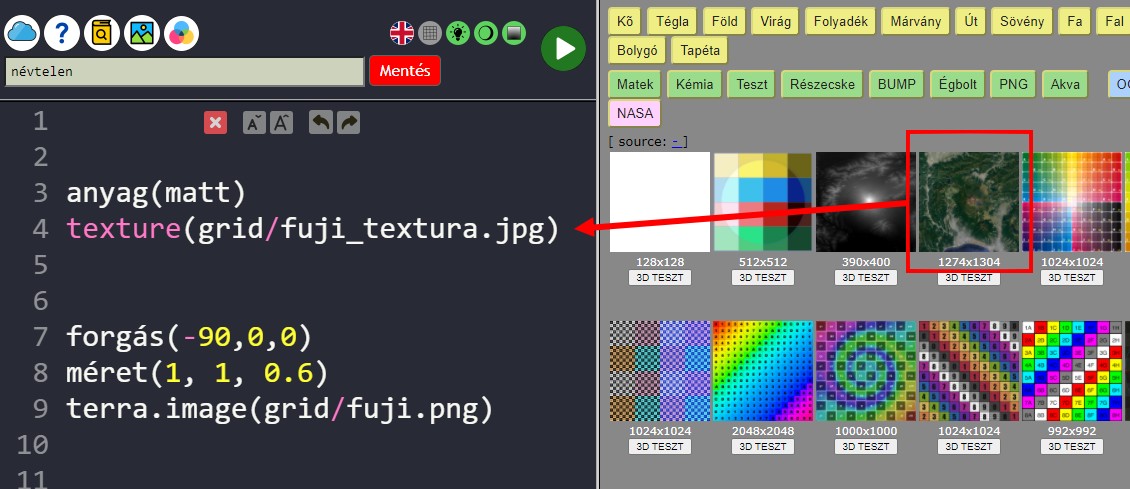
KÓD:
anyag(matt)
szín(fehér)
texture(grid/fuji_textura.jpg)
forgás(-90,0,0)
méret(1, 1, 0.6)
terra.image(grid/fuji.png)
Kattints a képre!
Mostantól JPG, vagy PNG fájlokat fel lehet tölteni a saját fiók tárterületre, beleértve a TESZT felhasználót is.
Lehetőleg a textúrák mérete osztható legyen 8-al. A legjobb az 512x512 pixeles méret. Ha gömb felszínre akarsz ismétlés nélkül textúrát helyezni, akkor a szélesség legyen duplája a magasságnak. (1024x512 pixel)
A fájl kiválasztása után indulhat a feltöltés. Figyelj a szabad területre!
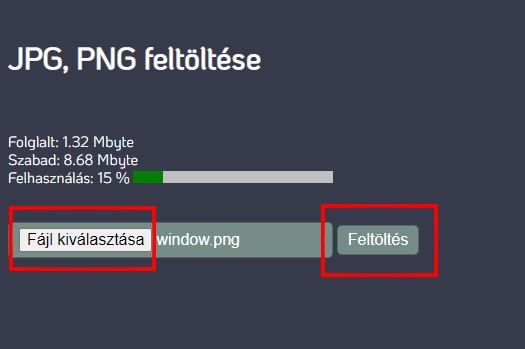
A feltöltött képek előnézete egy felugró ablakban jelenik meg. A kép nevére kattintva a forrásba kerül a textúra utasítás. JPG esetén normál textúra, PNG esetén átlátszó textúra lesz a kódban, de ezeket át lehet írni utólag. Az ismétlések száma után az utolsó paraméter a fiók neve lesz. Innen tudja a program, hogy a saját tárhelyedről kell betölteni a képet.
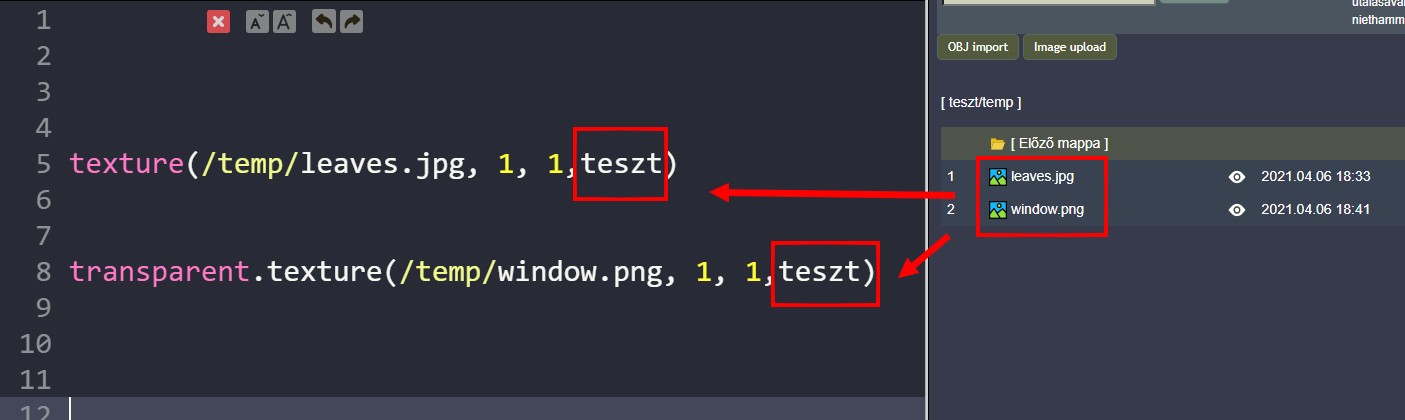
A kód:
texture(/temp/leaves.jpg, 2, 2,teszt)
hely(0,0,0)
tégla(20, 0.1, 20)
transparent.texture(/temp/window.png, 1, 1,teszt)
hely(0,4,0)
téglalap(8,8)
És a végeredmény:
A webglbasic egyik erőssége a geometria számítása matematikai képletekkel. A példában egy üvegből készült terráriumot fogok modellezni úgy, hogy minden adatot változókban, paraméterekben tárolok.
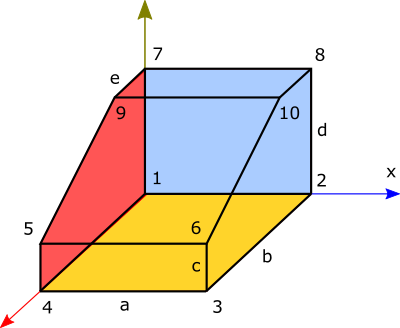
Célszerű először papíron vagy egy 2D rajzoló programmal lerajzolni a modellt. Ezután ráírtam a paraméterket. Ebben az esetben 5 db ilyen méret lesz lényeges:
a: szélesség
b: hosszúság
c: előlap magassága
d: magasság
e: tetőlap hosszúsága
Minden csúcs kap tetszőleges sorrendben egy sorszámot 1-től kezdődően. Ezek lesznek a felületek vertex pontjai.
Következő lépés a sík lapok háromszögekre bontása. Téglalapokat 2 db háromszögre lehet bontani, de az oldallapokat már 3 darabból kell összerakni.
A felületeket a vertex pontok felsorolásával lehet megadni. Célszerű azonos irányban haladva (pl. jobbra) haladva felsorolni a pontokat!
|
Például az alsó négyszög háromszögei: |
A baloldali lap háromszögei: 1 9 7, 1 5 9, és 1 4 5 |
A webglbasic kód elején megadjuk a paramétereket:
Ezután egy OBJ utasításban felsoroljuk a vertex pontokat. Az első pont sorszáma lesz 1. A pirossal jelölt sor a 3. pont koordinátái. A pont x,y,z koordinátái helyén számokat, és változókat is megadhatunk. Az adatokat csak 1 db szóköz válassza el egymástól!
 |
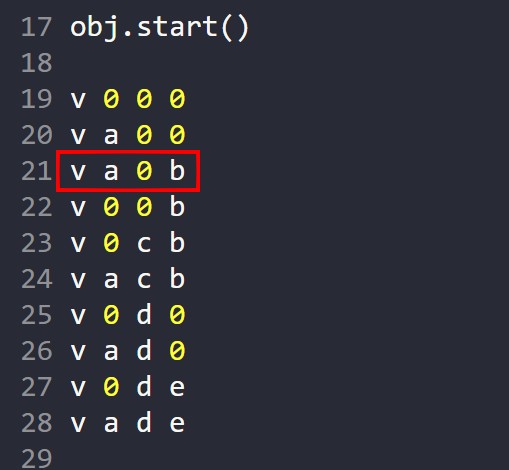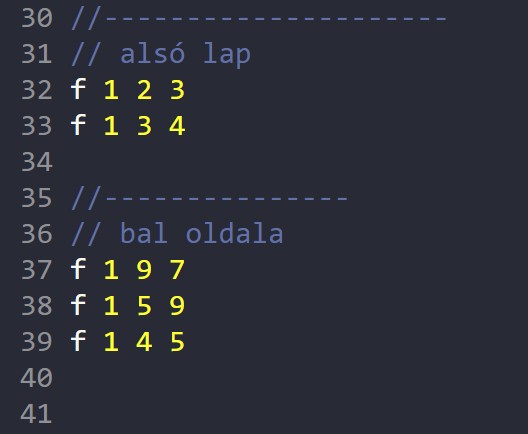
Ezután jöhetnek a felületek háromszögei:
|
A megfelelő nézőpont beállítása után beszúrhatunk a forrásba néhány kamera utasítást.
Végül lehet különböző paraméterekkel generálni a 3D modellt.
 |
 |
 |
A teljes kód:
color(#00bfff,#00bfff,#0,1,0.8)
a = 20
b = 10
c = 2
d = 10
e = 6
obj.start(2)
v 0 0 0
v a 0 0
v a 0 b
v 0 0 b
v 0 c b
v a c b
v 0 d 0
v a d 0
v 0 d e
v a d e
//---------------------
// alsó lap
f 1 2 3
f 1 3 4
//---------------
// bal oldala
f 1 9 7
f 1 5 9
f 1 4 5
//---------------
// jobb oldala
f 2 10 8
f 2 6 10
f 2 3 6
//---------------
// eleje
f 3 4 5
f 3 5 6
//---------------
// teteje
f 7 8 9
f 8 10 9
//---------------
// hátlap
f 1 7 2
f 7 8 2
obj.end
camera(KAM1, 25.66, 23.25, 41.04, 3.13, -0.74, -1.25)
camera(KAM2, -6.39, 30.53, 41.56, 8.37, -0.32, 0.31)
A Szilassi-poliéder egy konkáv poliéder hét hatszögletű lappal. A tetraéder mellett az egyetlen olyan ismert poliéder, amire teljesül, hogy bármely két lapjának van közös éle. Nevét Szilassi Lajos magyar matematikusról kapta, aki 1977-ben felfedezte.
Tengelyesen szimmetrikus, a szimmetria kétfogásos: egybevágó lappárjai vannak, és a hetedik lapnak ugyanaz a forgásszimmetriája, mint a testnek.
forrás: https://hu.wikipedia.org/wiki/Szilassi-poli%C3%A9der
3D modell:
